Schaumburgwelle/Raum Ith/Leinetal/SW (Südwest)

Name

Guido Hovestadt-Roser

Datum

05.10.2022

Windrichtung

SW (Südwest)

Ort des Wellensteiggebietes

Leinetal

Auslöser

Div.

Zeit-Bezugssystem

MESZ

Freier Bericht

Hatte heute morgen in Gronau / Leine zu tun ..... Fotos gegen 10 Uhr aufgenommen

 

Zusammenschau dokumentierter Flüge:

Jörg Dummann

 

Bei "www.Weglide.de" liegen 20 IGC-Files von Flügen am Wiehen-/Wesergebirge und Ith vor.
(Alle folgenden Zeitangaben Z, alle Höhenangaben MSL)
Die maximalen Hangflughöhen lagen bei ca. 600m.
Größere Höhen von 800 - 900m - einmalig bis 1.000m im Lee des Schaumburgwellen-Auslösers "Rumbecker Forst" - wurden thermisch erflogen.

(Anmerkung:
Ich verwende die Bezeichnung "Rumbecker Forst" für den Auslöser, da dieses mehrere Kuppen (Rumbecker Berg 340m, Taubenberg 300m, Herkenberg 301m, Hengstberg 289m, Bohrberg 286m) umfassende Gebiet lt. Topografischer Karte zusammenfassend so benannt ist.)

Die Landungen erfolgten - wohl wetterbedingt - frühzeitig, im Zeitraum von 12:00 bis 15:00, zum Großteil gegen 14:00 Uhr.
Es gab mehrere Versuche, den Einstieg in die "Schaumburg-Welle" zu finden:
vergeblich - oder die schwachen Steigwerte verschmähend - durch Peter von 11:00 bis 11:10, von Reinhard von 12:40 - 13:00 mit einem kurbelnd erreichten Höhengewinn auf 700m, Markus gegen 13:00 Uhr, ebenfalls belohnt durch einen Bart, von Niels vergeblich von 12:40 - 12:45, von Jan desgleichen 12:40 - 12-55 und von 14:00 bis 14:10 sowie vorher auch durch Knud von 13:50 - 13:55.

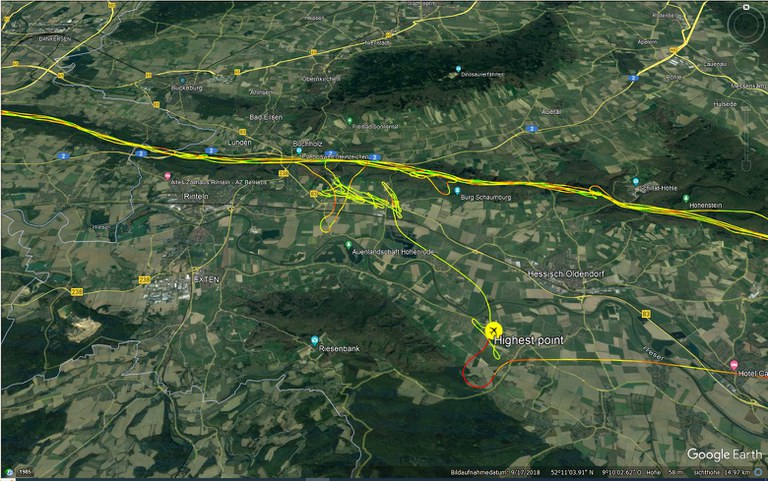
Knud konnte als Einziger aus einer Höhe von ca. 550m im Hangwindbereich durch Vorfliegen nach Luv das Steiggebiet der Schaumburgwelle über der Inversion gegen 11:00 Uhr erfolgreich erreichen und nutzen: gegen 11:30 erreichte er 1.600m MSL. Diese Höhe musste er - wohl um in VMC zu bleiben -  abrupt aufgeben und auf ca. 1.000m MSL (offenbar unter die Basis) absteigen.

 

Im Detail lässt sich der Aufstiegspfad in drei Phasen gliedern:

(Quelle: www.weglide.org)

 

Einstieg / Anfang Phase 1               570m MSL / 11:04:19
Ende Phase 1 / Anfang Phase 2      833m MSL / 11:12:32 ->  263m in 493s -> 0,53 m/s
Ende Phase 2 / Anfang Phase 3     1151m MSL / 11:17:18 ->  318m in 346s -> 2,47 m/s
Ende Phase 3 / Ausstieg               1600m MSL / 11:30:28 ->   449m in 790s -> 0,57 m/s

Unter Zugrundelegung eines minimalen Sinkens der ASH 26e von 0,5 m/s ergeben sich folgende Luftmassensteigwerte:

Phase 1: 1,03 m/s  also ca. 1 m/s

Phase 2: 2,97 m/s  also ca. 3 m/s

Phase 3: 1,07 m/s  also ca. 1,1 m/s

 

Der zweite mutmaßliche Wellenflug des Tages gelang Markus an m.E. ungewöhnlicher Stelle am Ith: in dem Bereich knapp südlich des Steinbruchs bei Bisperode (ich selbst habe dort nur einmal eine "Mikrowelle" (Höhe < 1.000m MSL) bei Südwind erlebt.): Markus stieg in dem Zeitbereich von ca. 13:10 bis ca. 13:30 dort von vorher thermisch am Ith-Hang erreichten 850m auf 1.700m.

Im Detail lässt sich der Aufstiegspfad in drei Phasen gliedern:

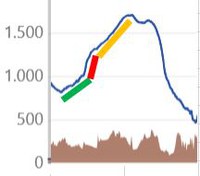
(Quelle: www.weglide.org)

 

Einstieg  / Anfang Phase 1              814m MSL / 13:08:35
Ende Phase 1 / Anfang Phase 2    1004m MSL / 13:15:32  ->   190m in 417s -> 0,46 m/s
Ende Phase 2 / Anfang Phase 3   1240m MSL  / 13:17:41  ->   236m in 129s -> 1,83 m/s
Ende Phase 3  / Ausstieg            1688m MSL  / 13:29:43  ->   448m in 722s -> 0,62 m/s

Unter Zugrundelegung eines minimalen Sinkens der ASW 15 von 0,6 m/s ergeben sich folgende Luftmassensteigwerte:

Phase 1: 1,06 m/s  also ca. 1 m/s

Phase 2: 2,43 m/s  also ca. 2,5 m/s

Phase 3: 1,22 m/s  also ca. 1,2 m/s

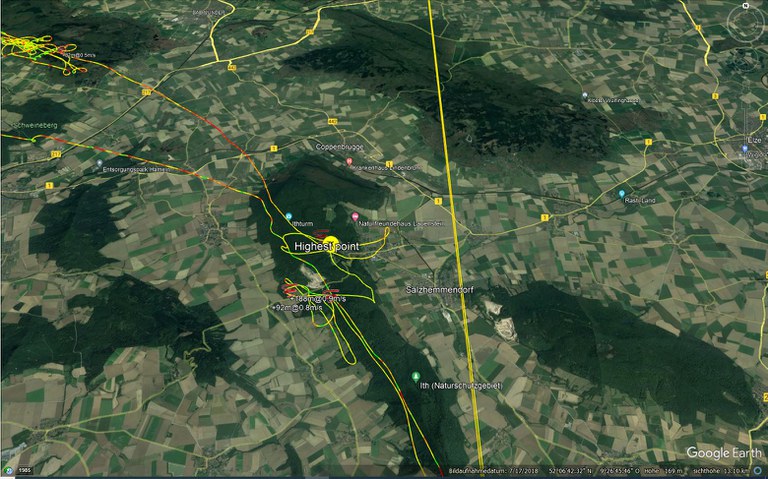
(Die gelbe Linie ca. 170/350° ist ein bei der Konvertierung IGC/KML entstandenes Artefakt.)

 

Doku der RASP-Vorhersage:

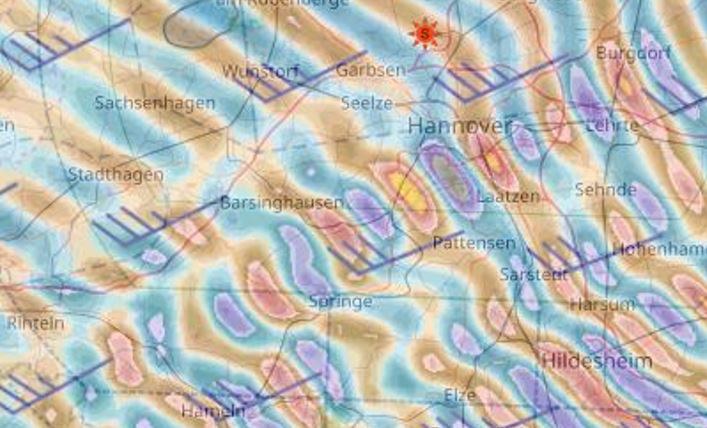
Auslöser der Schaumburgwelle (Rumbecker Forst) - Süntel - Deister in Resonanz...

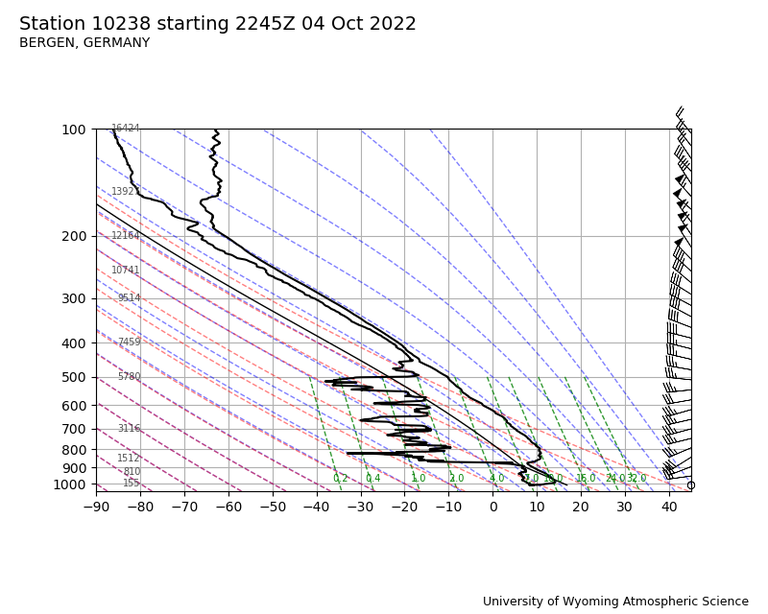
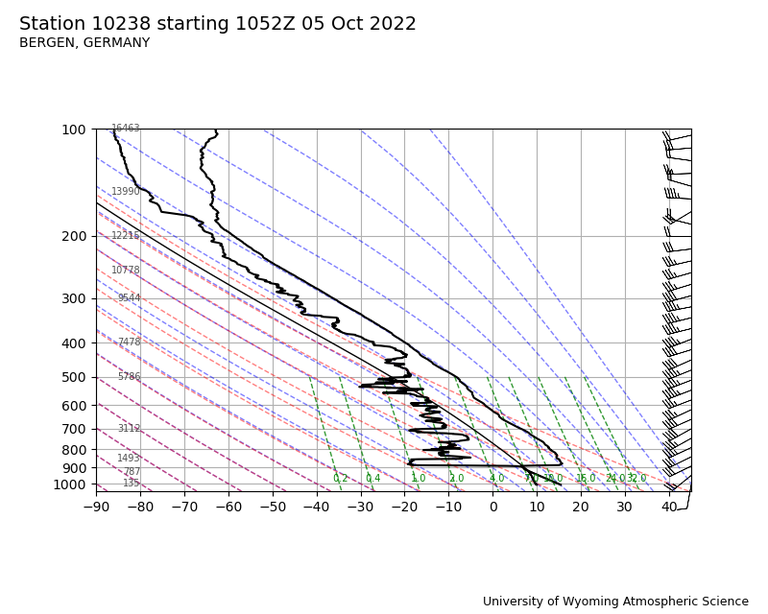
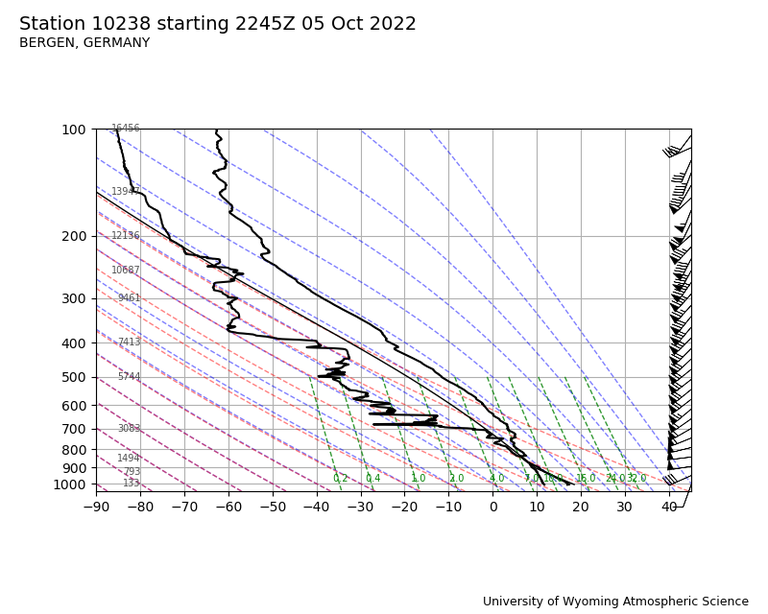
Schichtung:

Die zeitliche Entwicklung der von Bergen aus gemessenen Schichtung zeigt um 00:00 des 05.10.22 eine Inversion knapp über 1.000m, die sich im Mittagsaufstieg dann, etwas abgesunken, als ungewöhnlich scharf und stark ausgeprägt darstellt.

Der folgende mitternächtliche Aufstieg zeigt - wohl infolge eines spätnachmittäglichen Frontdurchgangs (die Recherche der synoptischen Situation habe ich mir erspart) - keine relevant ausgeprägte Inversion mehr.

Experimentelle Doku / Auswertung:

Jörg Dummann

Mit Vorsicht hier tituliert im Folgenden einige Ansätze, Gedanken und Auswertungen, die ich spannend finde - ohne Anspruch auf jedwede Professionalität!
Um Ansatzpunkte für Diskussionen zu liefern, etwas ausführlicher...

Die Ballonaufstiegsstation Bergen

liegt ungefähr 85 km entfernt ungefähr in Windrichtung im Flachland der norddeutschen Tiefebene.

Bei der aktuell knapp über Inversionshöhe registrierten Windgeschwindigkeit von ca. 15 m/s braucht eine Luftmasse vom Wesergebirge bis dort ca. anderthalb Stunden.

Es muss betont werden, dass durch diese räumliche und zeitliche Distanz nur grobe Schlussfolgerungen für die Beschaffenheit der Luftmasse am Wesergebirge zum Zeitpunkt der Wellenflüge möglich sind.
Hier muss Vorsicht walten, um nicht zu überinterpretieren.

Die Lage im Flachland hat den Vorteil, das der Sondenballon weniger wahrscheinlich in eine Wellenströmung gerät, die dessen Aufstiegsgeschwindigkeit durch Auf- oder Abwindströmungen modifizieren kann und so zu leicht fehlinterpretierbaren Messergebnissen führt. Viel wahrscheinlicher, dass so etwas passiert ist es z.B. bei der Aufstiegssatation Meiningen am Westabfall des Thüringer Waldes.

Da das auch bei der Station Bergen nicht vollständig ausgeschlossen werden kann, hier der Aufstiegspfad des Ballons als Höhe über MSL in der Abfolge der zeitlich konstant periodisch gespeicherten Messpunkte:

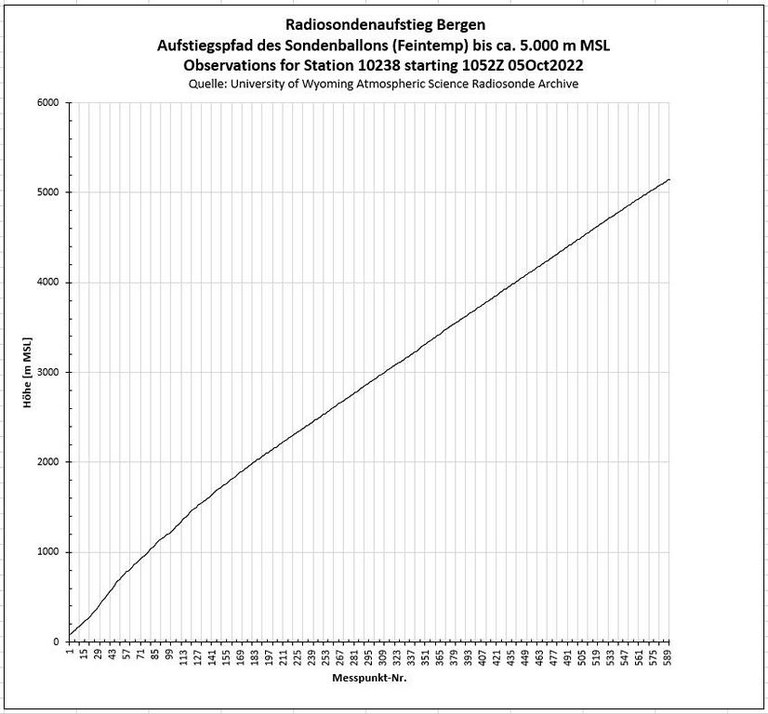
Der Pfad zeigt einen ungestörten Verlauf.

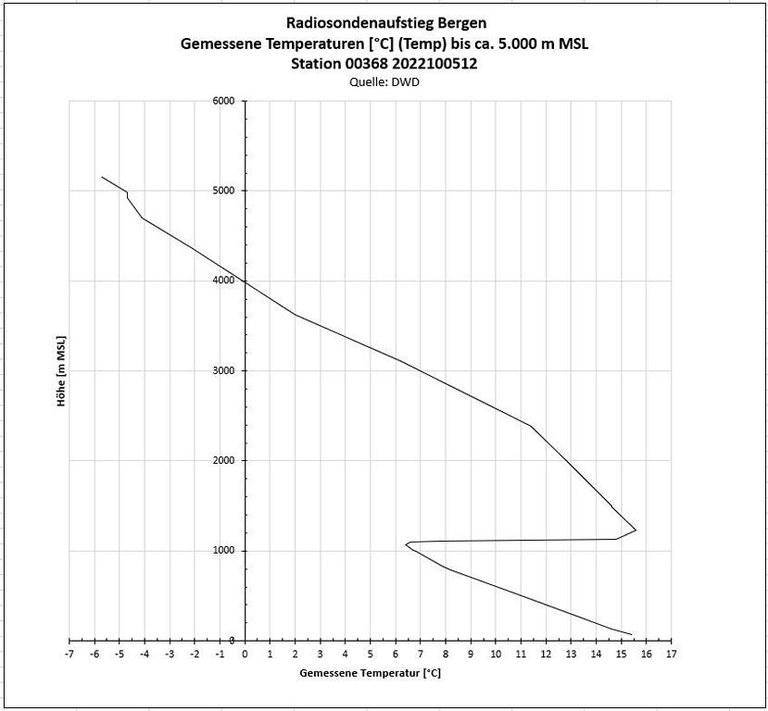
Temperatur

Auf der Website der Universtity of Wyoming liegen die Tempdaten in Form von Textfiles der Daten wie sie gemessen wurden, also nicht in Gestalt von auf markante Punkte hin geglätteten Verläufen vor, wie sie vornehmlich Verwendung finden.

So ist in Ergänzung zu den Temp-Abbildungen oben noch einmal eine präzisere Darstellung möglich.

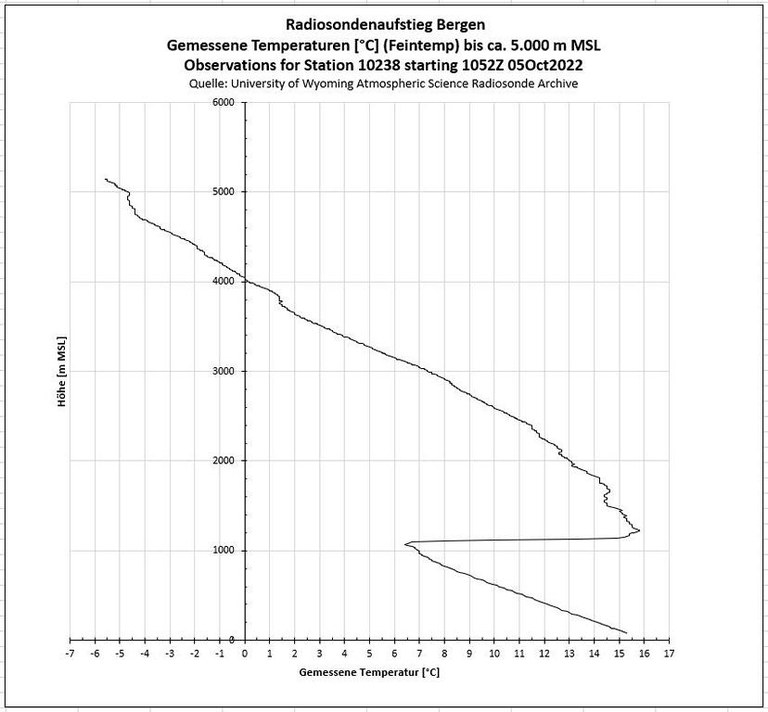
So wird der außerordentlich starke Anstieg der gemessenen Temperatur von ca. 9°C in einem sehr schmalen Höhenband der betrachteten Luftmasse augenfällig.

 

Nach Umrechnung in die trockenpotentielle Temperatur - das ist die Temperatur, die ein "Luftpaket" annehmen würde, wenn man es unter adiabatischer Erwärmung von ca. 1°C/100m aus seiner Höhe auf ein Druckniveau von 1.000 hPa herab versetzt - ergibt sich das folgende Bild.

Hierbei ist zu beachten, dass dieser Wert an Tagen mit Wolkenbildung nicht den natürlichen Verhältnissen entspricht, da der adiabatische Gradient durch Kondensations- und Verdunstungsprozesse modifiziert wird (Kondensatioswärme / Verdunstungskälte) Dies ist bei dem hier betrachteten 05.10.2022 der Fall. Die Berechnung ist mir z.Zt. nicht möglich bzw. zu aufwändig.

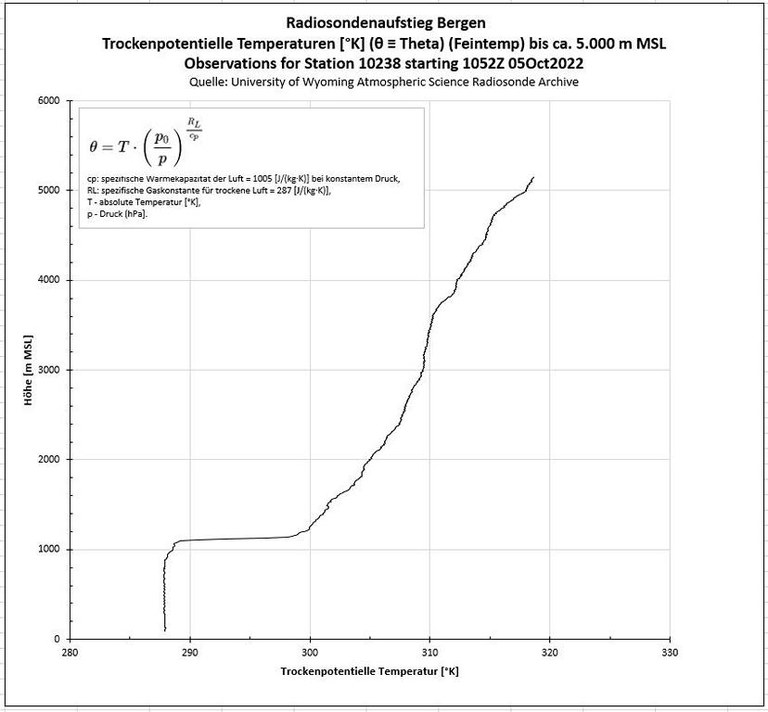
Diese Art der Darstellung lässt eine direkte Beurteilung der Stabilitätsverhältnisse (trocken!) zu:
Zeigt die trockenpotentielle Temperatur im vertikalen Verlauf keine Veränderung, ist das Folge der Tatsache, dass der Schichtungsgradient die Größe des trockenadiabatischen Gradienten aufweist. Wir stellen eine neutrale Schichtung fest.

Dies ist immer der Fall in einer Luftschicht in der sich dynamische oder thermische Konvektion abspielt - entweder durch mechanisch- oder thermisch-turbulente Durchmischung.

Ist der Graph des vertikalen Verlaufs der potentiellen Temperatur nach links geneigt, herrscht Labilität in der Luftmasse vor, ist er nach rechts geneigt, Stabilität.

So ist für uns erklärbar, dass es am 05.10. im Weserbergland möglich war, neben Hang- auch Thermik-Aufwind nutzen zu können. Übertemperaturen am Boden (die feuchte-Diskussion in diesem Zusammenhang lassen wir einmal außen vor.) ließen thermische Aufwinde bis an die Inversion zu - gleichzeitig haben diese die neutrale Schichtung der Luftmasse unterhalb der Inversion bedingt.

Dass auch an diesem Tag zwei Wellenflüge stattfanden, ist er ein neuerlicher Beleg dafür, dass die Luftmasse nicht bis hinunter zum auslösenden Leehang stabil geschichtet sein muss, um Leewellen entstehen lassen zu können. Auch wenn es unterhalb der Inversion durch die neutrale Schichtung nicht "schwingt" kann es oberhalb Wellen geben.

Ggfs. gerät an dieser Stelle unser Weltbild von dem Luftpaket, das in stabiler Schichtung durch das Übersteigen eines Bergkamms aus seiner Gleichgewichtslage ausgelenkt wird und sich - die Gleichgewichtslage trägheitsbedingt überschießend  - den Leehang hinab wieder in diese einpendelt, ins Wanken. Das ist ohnehin ein überdenkenswürdiger Ansatz, da ja alle Luftpakete in der Umgebung "unseres" Luftpakets das Gleiche machen... Zu diesen grundsätzlichen Fragen aber an anderer Stelle - später - mehr.

Wir können hier feststellen, dass es irgendeine "fernwirkende" Kraft gibt, die Wellen in der Luftmasse über der neutralen bodennahen Schicht auslöst.

Die Schichtung in der Bodenluftschicht unter der Inversion hat großen Einfluss darauf, wie wir den Einstieg in die Welle finden können.

Ist sie ebenfalls stabil, dann gelingt der Einstieg auch unterhalb der Inversion problemlos. Häufig ist es dann in unseren Mittelgebirgsleewellen so, dass sich Hang- und Wellenaufwind überlagern (kann aber auch der gegenteilige Fall sein.) Ist sie weniger stabil wird es immer problematischer: solange noch geringe Stabilität vorhanden ist, kann man sich einigermaßen zuverlässig in Rotorthermik nach oben hangeln, was den Vorteil hat, dass man seine Position in der Welle einschätzen kann. Ist es vollständig neutral, bleibt nur, dass man im Hangaufwind und/oder thermisch die für den Einstieg in die Welle nötige Höhe erreicht. Unter Umständen muss man dabei dann auch noch Glück haben, dass die Welle auch gerade "da" ist - nicht immer ist die Wellenströmung stabil, es kann dazu kommen, dass die Welle fluktuiert - mal mit dem Wind abtreibt, mal sich neu formiert...

Diese abschließend geschilderten Bedingungen kennzeichneten womöglich die Situation am 05.10. im Weserbergland.

Wind

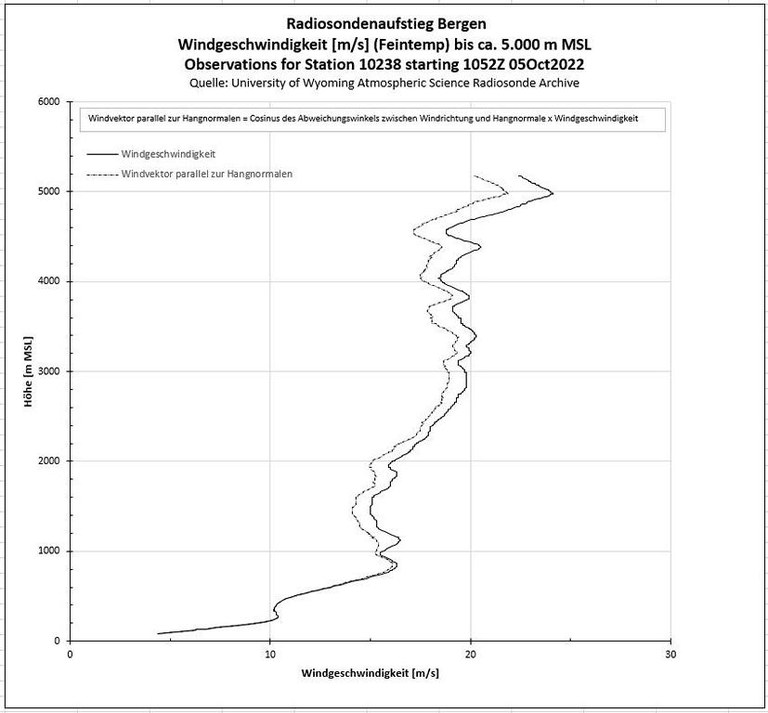
In der Reibungsschicht unterhalb der Inversion sehen wir eine deutliche Zunahme der Windgeschwindigkeit bis zur Inversion.

In der Schicht darüber von ca. 1.000m bis 2.000m eine "variable Konstanz" des Windes.

Diese kann ich in ihrer Bedeutung für die Wellenausbreitung nicht einschätzen. Sie ergibt sich ohnehin im Zusammenspiel von Wind und Stabilität der Luftmasse (vgl.u.)

Getrichelt dargestellt ist oben der in Richtung der Hangnormalen des auslösenden Höhenzuges wirkende Anteil der Windgeschwindigkeit.
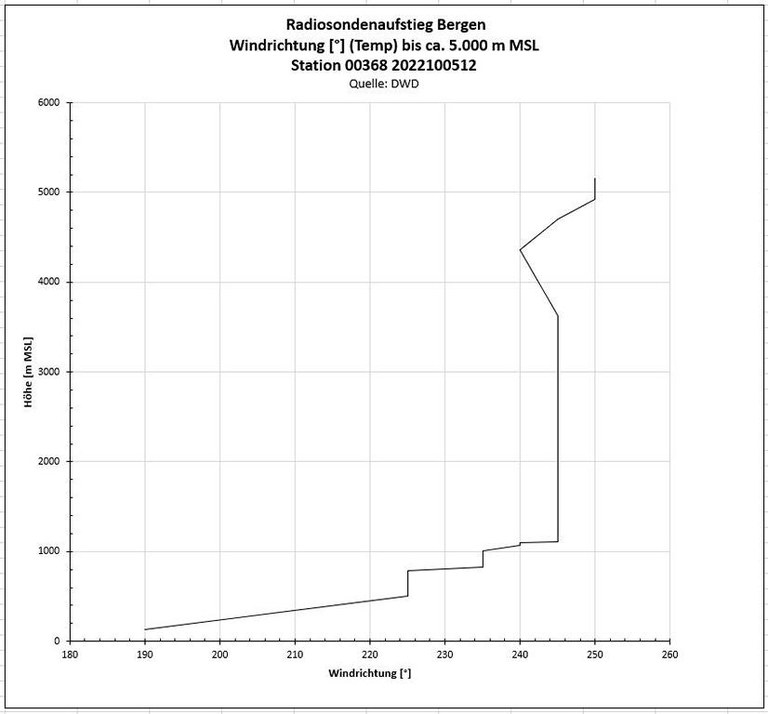
Der Leehang des Rumbecker Forst ist nach 45° exponiert, was heißt dass sie luvseitig nach 225° ausgerichtet ist - fast in Windrichtung, die Auswirkung auf den rechtwinklig zum Kammverlauf wirkenden Windvektoranteil ist also gering und birgt auch im Höhenverlauf keine Überraschungen. Dies ist auf den wenig variablen Verlauf der Windrichtungsdaten mit der Höhe zurückzuführen:
(Der Bereich des Einstiegs von Knud ins Wellensteigen liegt im Lee des nördlichen  - sich mehr in Richtung W/E erstreckenden - Teils des Rumbecker Forsts. Die sich dadurch ergebende größere Abweichung von der Höhenwindrichtung wurde hier nicht erfasst.)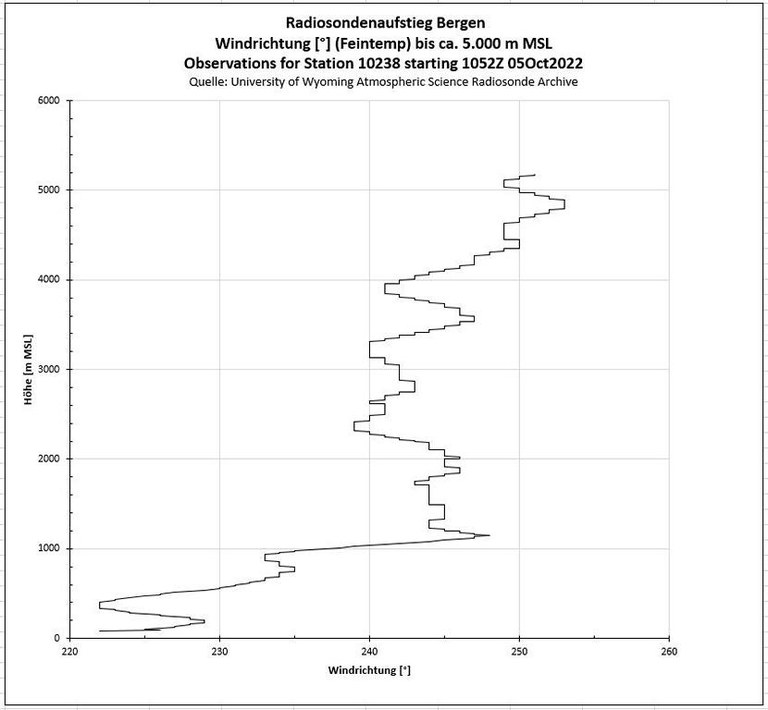

Unterhalb der Inversion ist eine mit Höhen- und Geschwindigkeitszunahme verlaufende Rechtsdrehung des Windes zu verzeichnen.
IWie die Abbildung oben ("Windvektor parallel zur Hangnormalen") zeigt, hat dies in Verbindung mit den unten geringeren Windgeschwindigkeiten kaum einen Effekt.
Insbesondere hier stellt sich aber die Frage, ob diese Daten aus dem 85km entfernten Flachland einfach zu übertragen sind.

 

Dichte

Interessant auch, inwieweit der ausgepägte Temperatursprung im Bereich der Inversion den Verlauf der Dichte beeinflusst:

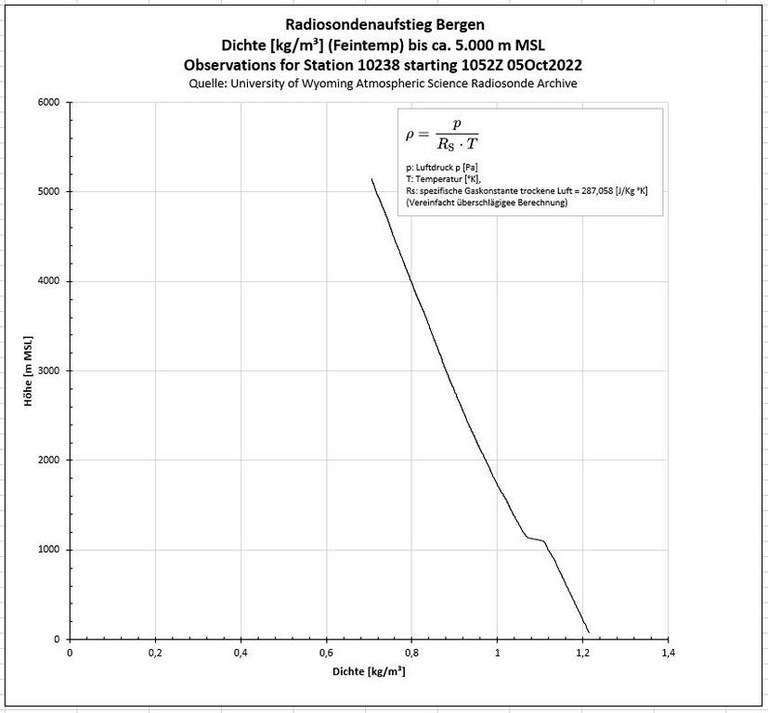
Hier berechnet in einem vereinfachten Verfahren für trockene Luft und Betrachtung derselben als ideales Gas.

 

"Schwingungsfähigkeit"

Die Brunt-Väisälä-Frequenz (hier: BV-Frequenz) ist ein Maß zur Quantifizierung des auch in Segelfliegerkreisen oft bemühten und dort "Schwingungsfähigkeit der Luft" genannten Parameters.
Die Formulierung der mathematischen Funktion (vgl. Diagramm unten), welche das Zusammenspiel der physikalischen Faktoren ausdrückt, gelang unabhängig voneinander sowohl David Brunt als auch Vilho Väisälä.
Vilho Väisälä war insbesondere im Zusammenspiel mit der von ihm betriebenen Entwicklung und dem Einsatz von Wetterballons an den Mechanismen interessiert, wie sich separate "Luftpakete" in unterschiedlichen Schichtungen verhalten.
Die Lösung, wie sich sowohl die Größe der Potentiellen Temperatur selbst als auch deren Gradient mit der Höhe dabei als steuernde Größen zeigen veröffentlichte er im Jahr 1932.

Die BV-Frequenz ist eine weitgehend abstrahierte Angabe, die sich darauf bezieht, welcher Winkelbereich von einem im Einheitskreis mit einer bestimmten Geschwindigkeit rotierenden Zeiger in einer Sekunde überstrichen wird. Deswegen wird dieser Wert auch Kreisfrequenz oder Winkelfrequenz genannt.

 
Die Zeit, welche bei einer gegebenen Kreisfrequenz für einen Vollumlauf des Zeigers benötigt wird, errechnet sich aus derselben durch Division von 2pi durch die Kreisfrequenz, hier: BV-Frequenz.
Der erhaltene Wert ist identisch mit dem Wert, den eine Schwingung auf einem Zeitstrahl benötigt, um z.B. von Maximum zu Maximum zu schwingen. Das ist der Wert, der landläufig als "Frequenz" bezeichnet wird.

Für das Verständnis der BV-Frequenz ist es wichtig zu erkennen, dass diese (primär) nichts mit der Größe der Auslenkung eines Luftpakets aus seiner Gleichgewichtslage zu tun hat. Diese ist beliebig. Somit kann auch die Amplitude einer Welle nicht über die BV-Frequenz bestimmt werden.

Die BV-Frequenz ist z.B. identisch für die folgenden drei Fälle:

ein sich adiabatisch abkühlendes Luftpaket wird um 1.000m vertikal nach oben ausgelenkt und die Temperatur der umgebenden Luftmasse sinkt dabei um 6,5°C
oder es wird um 100m nach oben ausgelenkt und die Temperatur der umgebenden Luftmasse sinkt dabei um 0,65°C
oder es wird um 10m nach oben ausgelenkt wird und die Temperatur der umgebenden Luftmasse dabei um 0,065°C sinkt.

Mein Versuch, nun den Verlauf der BV-Frequenz mit der Höhe anhand der Daten aus dem Feintemp zu ermitteln und darzustellen, endeten erst einmal in einem Rätsel: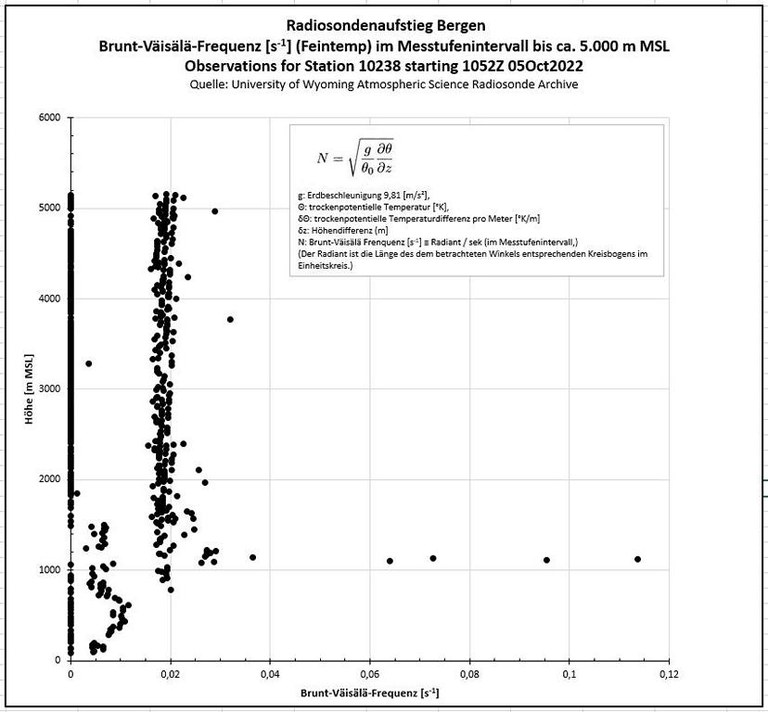

 

Der erhoffte detaillierte Verlauf zeigte sich nicht. Eine Darstellung bei der die errechneten Werte durch Linien verbunden sind, führte zu einem dichten Wirrwarr im Bereich BV-Frequenz 0 bis 0,02.
Deswegen hier die Darstellung nur der Werte, ohne Verbindungslinien. So zeigt sich, dass bei den geringen Höhenunterschieden der der Berechnung zugrundeliegenden Messpunkte, häufig keine Änderungen der Potentiellen Temperatur eintraten, also deren Gradientwert Null ist. Dies führt zu einer Aufspaltung der eigentlich harmonisch verlaufenden Entwicklung der BV-Frequenz in "On" / "Off"-Punkte, quasi einer Digitalisierung des analogen Ablaufs. Die Werte >0 sind nicht korrekt, wie die unterhalb der Inversion augenfällig zeigen: hier ist die Schichtung neutral, eine vertikale Oszillation also nicht möglich.

 

Es liegt die Vermutung nahe, dass der "Scale" der Auswertung in etwa dem des zu untersuchenden Phänomens entsprechen sollte.

 

Zum Glück liefert der DWD Temps, die per Algorithmus auf ihre markanten Punkte reduziert wurden:

 

 

 

 

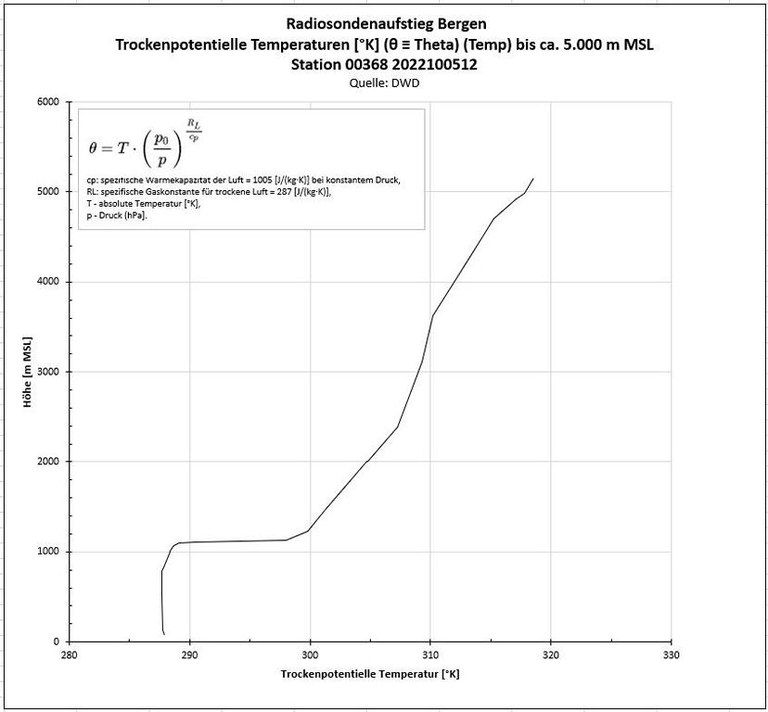
Auch hierbei wird die hypothetische Forderung nach möglichst weitgehender Ähnlichkeit von Auswertungs- und Phänomen-"Scale" nicht in optimaler Weise erfüllt werden.

 

Für die vertikale Verteilung der BV-Frequenz ergibt sich nun folgendes Bild:
Richtig dargestellt ist nunmehr, dass sich in der neutralen Schicht unter der Inversion keine Wellen bilden können.
 

 

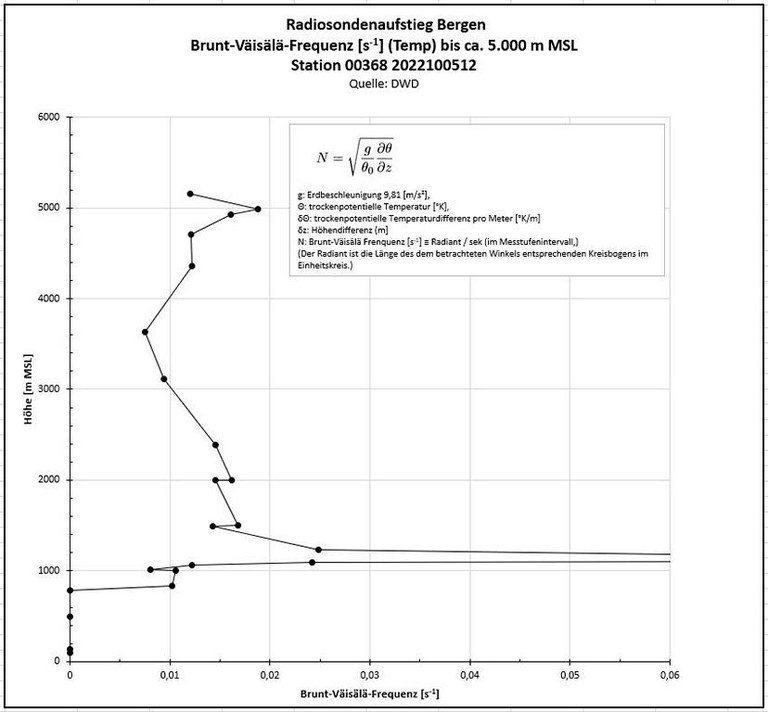
Für etwas mehr Anschaulichkeit sorgt die Errechnung und Darstellung der Schwingungsdauer:

 

 

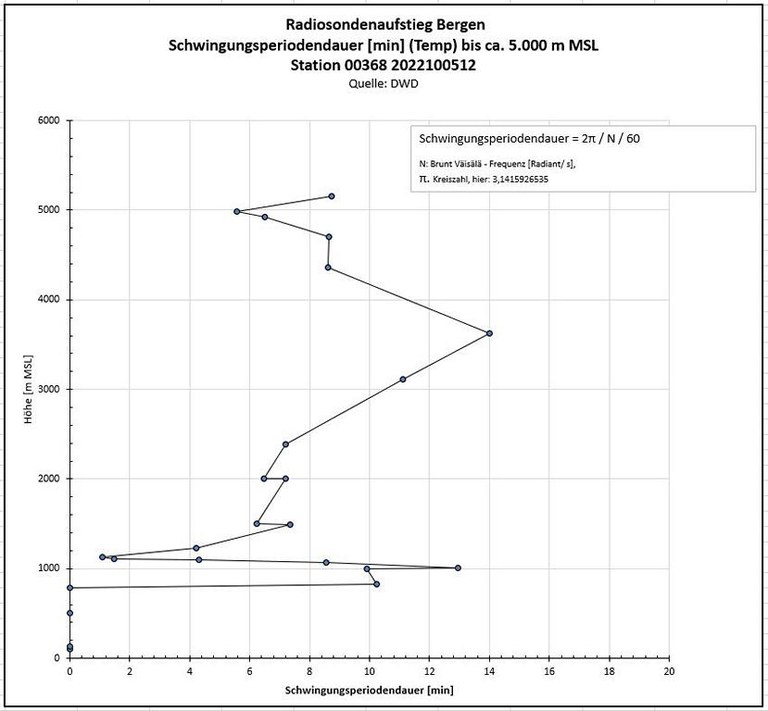
Für noch mehr Anschaulichkeit sorgt die Errechnung und Darstellung der vertikalen Verteilung von Längen stationärer Wellen.

 

Aber Achtung; hier ist vorerst Vorsicht geboten:
Entgegen einem gängigen, sogar in unseren Lehrbüchern und auch in vielen Vorträgen verbreiteten Trugschluss, gibt es in diesem Universum keine Welle, deren intrinsische Ausbreitungsgeschwindigkeit ("Phasengeschwindigkeit") von der Geschwindigkeit des Mediums, in dem sie sich ausbreitet, bestimmt wird. Diese sogenannte "intrinsische Phasengeschwindigkeit" auch einer atmosphärischen Schwerewelle hängt nicht von der Advektionsgeschwindigkeit - sprich: Windgeschwindigkeit - der Luftmasse ab, in der sie sich ausbreitet.

Aber: Gebirgswellen sind stationäre Wellen, sie sind ortsfest.(Bitte nicht verwechseln mit "Stehenden Wellen", das sind Wellen, die - meist durch gegenläufige Überlagerung - über keine Orbitalbewegung verfügen.)

Und diese Ortsfestigkeit entsteht dadurch, dass ihre Ausbreitung entgegengesetzt zum Versatz der Luftmasse erfolgt, mit gleicher Geschwindigkeit. Wenn man denn so will, ist die - nicht-intrinsische - Ausbreitungsgeschwindigkeit solcher Wellen unter Berücksichtigung der Geschwindigkeit des Mediums gleich "Null".

Das heißt nicht, dass es nicht Gebirgswellen gibt, die andere Ausbreitungsgeschwindigkeiten als solche haben, welche die Windgeschwindigkeiten gerade kompensieren. Aber diese schwimmen entweder mit der Luftmasse ab (falls sie langsamer sind) oder wandern gegen diese vor (falls sie schneller sind). Beide Fälle bedeuten, dass sie unauffälliger bleiben, sich nicht zu der Intensität einer stationären Welle aufbauen können.

 

So zeigt denn die nachfolgende Grafik auch nicht die Wellenlänge tatsächlich vorhandener stationärer Leewellen an, sondern die Wellenlängen, die sie in den entsprechenden Höhen hätten, falls ihre intrinsiche Ausbreitungsgeschwindigkeit genau umgekehrt gleich der Windgeschwindigkeit wären.

 

Dies ist auch der Grund, warum Faustregeln funktionieren, welche von der Windgeschwindigkeit auf die Wellenlänge schließen - mit korrekten Ergebnissen.
Aber Vorsicht - die Mathematik fragt nicht nach Kausalitäten!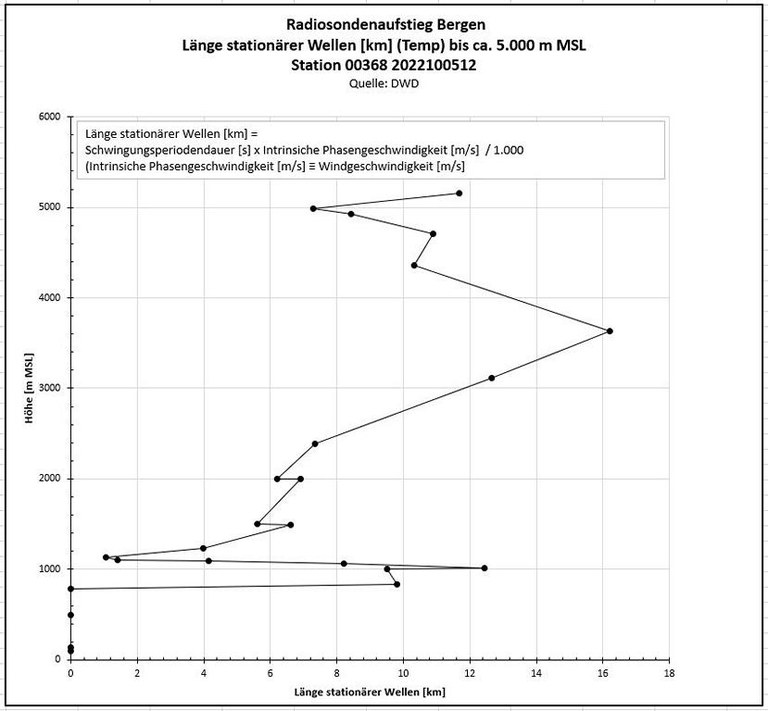

 

 

Für die obige Berechnung wurde die DWD-Windgeschwindigkeit wie folgt verwendet:

 

 

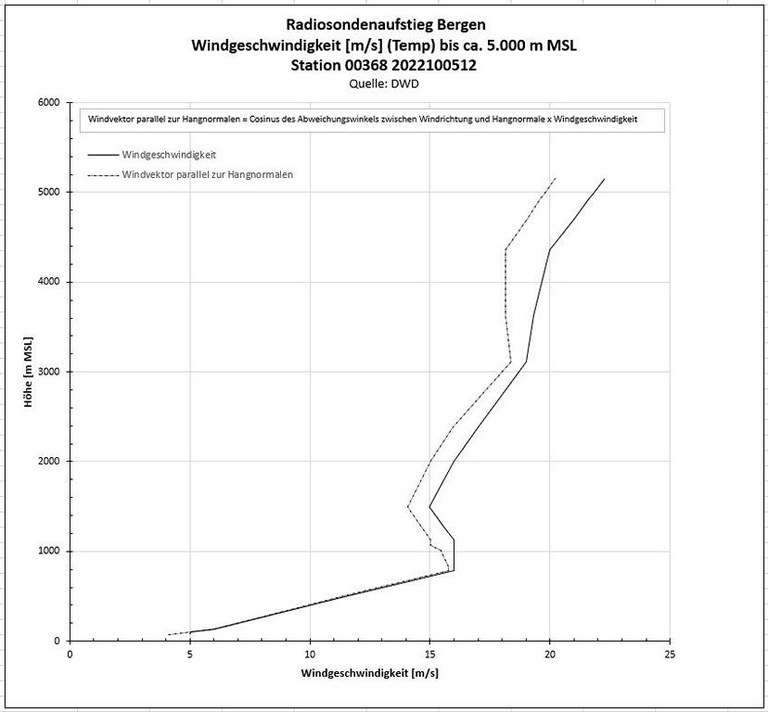
 Zur ergänzenden Info: die DWD-Windrichtung

 

 

Scorer Parameter

 

Was Richard Scorer hier in den vierziger Jahren des letzten Jahrhunderts getan (und im Jahr 1949 veröfentlicht) hat, ist, dass er eine auf die Zeit bezogene Kenngröße einer Welle, letztlich die Frequenz in Gestalt der BV-Frequenz, auf eine räumliche Größe bezogen hat: die Länge des Windvektors. Dieser Kunstgriff ist möglich - wie oben schon ausgeführt - da der Betrag der Länge des Windvektors bei stationären (ortsfesten) Wellen mit dem der Wellenausbreitungsgeschwindigkeit gleich zu setzen ist. Das Ergebnis dieser Berechnung ist in der Wellenphysik allgemein als "Wellenzahl" bekannt. Die Wellenzahl ist der Kehrwert der Wellenlänge. Sie sagt aus, wie oft die Wellenlänge in einen Meter hineinpasst (vgl. dazu die Maßeinheit [1/m]). Sie ist das räumliche Analogon zur zeitlich bezogenen Frequenz, die ausssagt, wie oft die Periodendauer einer Welle in eine Sekunde hineinpasst [1/s].

Worüber der Scorer Parameter in seinem Höhenverlauf also letztlich Aussage trifft, ist die Abfolge von Wellenlängen, wie sie sich aus der Stabilitätsverteilung und den über die Windgeschwindigkeit definierten Ausbreitungsgeschwindigkeiten der Wellen ergeben. Es ist intuitiv einzusehen, dass sich ein Wellensystem nur dann harmonisch nach oben ausbreiten kann, wenn die Wellenlängen nicht zu stark voneinander abweichen.

Nimmt der Scorer Parameter größere Werte an, bedeutet dies eine Abnahme der Wellenlänge (und entsprechend umgekehrt).

Für ein Wellensystem, das sich in größere Höhen erstreckt, sollte man also eine Konstanz des Scorer-Parameters erwarten.
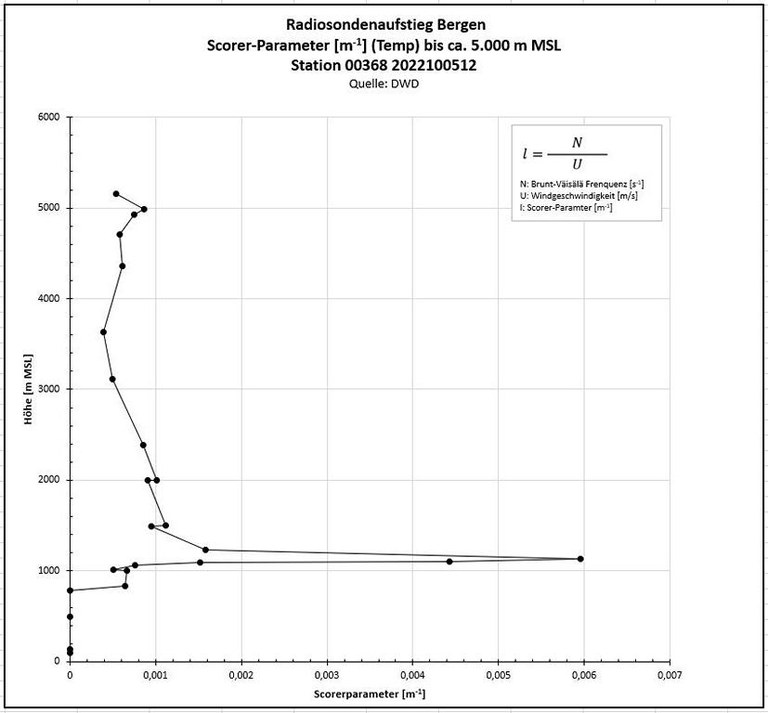
Die uns mitgeteilte Faustregel besagt, dass der Scorer Parameter mit der Höhe leicht und regelmäßig abnehmen sollte.
Im vorliegenden Fall beobachten wir dies bis in eine Höhe von ca. 3.600m, wobei allerdings in Höhen von ca. 1.500m und ca. 2.000m Inkonsistenzen im Verlauf auftreten.
Ob dies schon zu einem Bruch in der vertikalen Wellenstruktur führt, vermag ich nicht zu sagen. (Genau solche Fragen sind "raison d'être" für diese Ausführungen. :-))

Evtl. steht ja das Scheitern des weiteren Aufstiegs bei beiden Flügen zwischen 1.600m und 1.700m damit in Zusammenhang? Bei dem Versuch, solch präzise Schlüsse ziehen zu wollen, müssen wir uns aber der großen zeitlichen und räumlichen Distanz des Temp-Aufstiegs von dem Ort des Geschehens und darüber hinaus auch der vollzogenen Reduktion der Daten im Temp-Verlauf auf markante Punkte bewusst sein. Ob dieser Verlauf letztlich Merkmale in einem "Scale" berücksichtigt, die für den "Scale" des Phänomens von Bedeutung sind, muss mit Vorsicht betrachtet werden.

 

Der Verlauf des Scorer Parameters im Höhenbereich der Inversion ist insofern von Relevanz, als er deren Existenz anzeigt.

 

 

Analog zur Umrechnung der Kreisfrequenz (BV-Frequenz) auf die Schwingungsperiodendauer wird die Schwingungsperiodenlänge, also kurz die Wellenlänge, durch Division von 2pi durch die Wellenzahl (Scorer Parameter) ermittelt.
Glücklicherweise sieht man, dass der Graph unten identisch ist mit dem anschaulich "küchenphysikalisch" ermittelten in der Abbildung "Länge stationärer Wellen" (oben).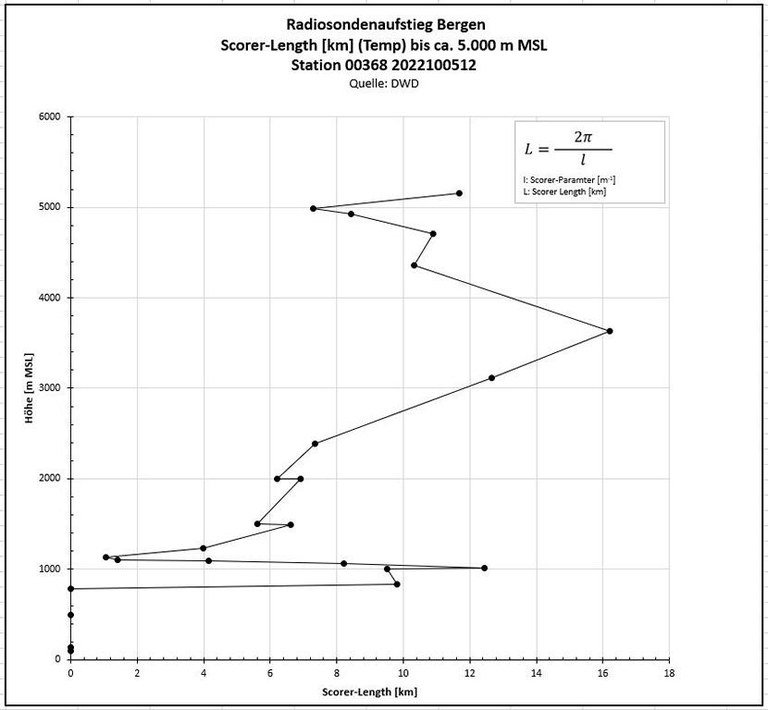

 

 

Mit großem Dank an Dieter Etling, dessen auf der Schwerewellen-Site veröffentlichte Buch "Atmospheric Gravity Waves and Soaring Flight - Physical principles and practical applications" hier sehr geholfen hat - und für besser Eingeweihte als mich noch so viele Schätze beeit hält...

 

Phasengeschwindigkeit (Intrinsische Wellenausbreitungsgeschwindigkeit)

 

Die nachfolgend beschriebene Möglichkeit, die Phasengeschwindigkeit einer externen Schwerewelle - also einer, die an eine Diskontinuität im vertikalen Temperatur- bzw. Dichteverlauf, also eine atmosphärische Grenzfläche,  geknüpft ist - zu berechnen, kann m.E. in den Kontext der oben mehrfach genannten hypothetischen Prämisse gestellt werden, dass nämlich der Scale der der Auswertung zugrundeliegenden Daten mit dem der untersuchten Gebirgswelle in Einklang stehen muss.

Es geht - hier exemplarisch nach G. J. MAYR, A. GOHM, Schnelle Strömungen durch Gebirgseinschnitte, promet, Jahrg.32, Nr. 1/2, 11-17 (März 2006) - darum, die Phasengeschwindigkeit einer Gebirgswelle an einer Inversion über die Dicke der unter ihr befindlichen Schicht, der durchschnittlichen potentiellen Temperatur dort und der Differenz dieses Wertes zur durchschnittlichen potentiellen Temperatur in der entsprechenden Schicht über der Inversion, zu bestimmen.
Die Mächtigleit der Inversionsschicht selbst, die mutmaßlich ebenfalls einen großen Einfluss haben dürfte, wird - bewusst - vernachlässigt und als "dünn" vorausgesetzt.

Anhand des Feintemps habe ich die Höhenlage der Inversion - immer noch +-willkürlich - zwischen 1.108m und 1.179m eingeordnet.
Das ergibt eine Dicke von 1.108m für die Mächtigkeit der unteren Schicht. Alle Messwerte dort berücksichtigend ergibt sich die durchschnittliche Potentielle Temperatur dort als Summe all dieser dividiert durch die Anzahl der Messpunkte (hier:86). Sie beträgt 288,01°K. In der mit entsprechender Mächtigkeit (bis in eine Höhe von 2.194m) berücksichtigten Schicht oberhalb der Inversion errechnet sich der Durschschnitt der Poteteiellen Temperatur aus 112 Messpunkten mit 303,22°K. In die Formel eingesetzt liefert diese einen Wert von 22,9 m/s. Dies ist ein deutlich höheren Wert als der, nach dem wir anhand der Windgeschwindigkeitsverteilung stationäre Wellen an der Inversion erwarten können (vgl.o.).

Mich erinnernd, dass der größte Teil der unteren Schicht aufgrund der neutralen Schichtung dort gar keine Wellen führen kann, habe ich die Berechnung erneut durchgeführt: nunmehr beschränkt auf den oberen Teil der oberen Schicht, in dem reale Werte für die BV-Frequenz tatsächlich gegeben sind.
Dabei ergibt sich eine Mächtigkeit der unteren Schicht von 309m. Die mittlere Potentielle Temperatur dort errechnet sich aus 29 Messwerten mit 288,26°K (also kaum ein Unterschied). In der entsprechend mächtig angenommenen Schicht oberhalb der Inversion (bis 1.493m) ergibt der Durchschnitt aus ebenfalls 29 Messwerten eine mittlere Potentielle Temperatur von 300,54°K (somit einen Unterschied von fast -3°K zur dicker angenommenen Schicht bei der Erstbetrachtung). Sowohl durch den letztgenannten Effekt, aber wohl insbesondere durch die geringer angenomme Mächtigkeit der unteren Schicht, ergibt ein im Vergleich zur Erstberechnung ungefähr halbierter Wert für die Ausbreitungsgeschwindigkeit i.H.v. 11,36 m/s. Ein Wert im ungefähren Größenordnungsbereich der Wingschwindigkeiten von ca. 15 m/s im Inversionsbereich und darüber (vgl.o.).

Alles in Allem wird hier Wohl und Wehe der Forderung nach den übereinstimnmenden Scales bei Auswertung und Phänomen deutlich: um das eine zu veranschlagen, muss ich das andere kennen.
Hier sollten wir der Versuchung widerstehen, rückwärts zu schließen...

Amplitude

  
Im Unterschied zu den bisher abgehandelten Wellenparametern entzieht sich die Amplitudengröße einer Bestimmung über die bisher diskutierten Faktoren. Sie ist zwar auch abhängig von den Schichtungsverhältnissen in der Atmosphäre, aber in größerem Maße auch von der Intensität des Auslöseimpulses der Welle oder auch von komplexeren Vorgängen stromaufwärts der betrachteten Welle, wie sie etwa in Gestalt von Superpositionseffekten mit Wellen von luvwärts gelegenen Auslösern auftreten können.
Hier können wir uns allerdings auf die Flugweg-Daten der beiden Flüge.stützen, um Angaben über die Amplitude zu gewinnen.
Grundsätzlich zeigt sich bei den Wellenaufstiegen im Rahmen beider Flüge eine ähnliche Struktur: im unteren Bereich herrscht schwächeres Luftmassensteigen um 1 m/s vor. Ein Wert der sich - etwas erhöht auf 1,1 bzw. 1,2 m/s - im oberen Drittel der Welle wiederfindet, oberhalb des mittleren Bereichs, in dem deutlich höhere Steigwerte von 3 bzw. 2,5 m/s anzutreffen sind, Bei näherer Betrachtung ergeben sich jedoch erstaunlicherweise grundlegende Unterschiede.
Im Einzelnen:
für die Welle am großen Ith-Krücken Steinbruch mit unbekanntem Auslöser:
Phase 1: ab   814 m, 263 m mächtig, ca. 1 m/s
Phase 2: ab 1.004 m, 236 m  mächtig, ca. 2,5 m/s
Phase 3: ab 1.240 m, 448 m mächtig, ca. 1,2 m/s
für die Schaumburg-Welle:
Phase 1: ab   570 m, 190 m mächtig, ca. 1 m/s
Phase 2: ab   833 m, 318 m  mächtig, ca. 3 m/s
Phase 3: ab 1.151 m, 449 m mächtig, ca. 1,1 m/s

Die Übergänge zwischen den Schichtbereichen mit unterschiedlichem Luftmassensteigen erfolgen nicht harmonisch fließend. Dies hätte man als Folge der in der Nähe des Wellentals und des Wellenkamms abklingenden Steigungen der Strömung innerhalb einer singulären Oszillation interpretieren können. Die Wechsel der Steigwerte vollziehen sich eher deutlich abgrenzbar und zudem bei beiden Flügen in ähnlichen Schichtdicken, so dass hier von drei unterschiedlich oszillierenden Systemen ausgegangen werden soll. Plausibel ist es anzunehmen, dass die größten Auslenkungswerte im Bereich der Inversion auftreten, welche Leiter der externen Schwerewelle / Gebirgswelle ist.

Hinweisen möchte ich darauf, dass die Abgrenzung der o.a. Phasen unabänderlich einer gewissen Willkür unterliegt. Die genannten präzisen Werte entsprechen einfach Loggerpunkten in den IGC-Files und spiegeln eine hohe Genauigkeit nur vor. Ausgehend von diesem Sachverhalt sind die nachfolgenden Betrachtungen mit einer gewissen Unsicherheit behaftet.

Konkret können wir zunächst die ermittelten Aufwindgeschwindigkeiten mit den bekannten Windgeschwindigkeiten in Beziehung setzen, um Rückschlüsse auf die Steigung des aufsteigenden Wellenteils treffen zu können.

Durch Division des Werts sowohl der Aufwindgeschwindigkeit (hier 2,5 m/s) als auch der Windgeschwindigkeit durch den der Windgeschwindigkeit (welche dem Winkel der Wellenströmung folgt, hier: 15 m/s) reduzieren wir das Verhältnis beider auf eines im Einheitskreis und erhalten so anstatt der Aufwinds den Sinuswert des Winkels, den die ansteigende Wellenströmung mit der Horizontalen einschließt.

Hierzu muss man feststellen, dass dieses Modell eine sehr starke Vergröberung und Idealisierung der realen Verhältnisse bedeutet. Es ergibt sich ein Gebiet mit einem gleichmäßig verteilten Luftmassensteigen für die halbe Wellenlänge. Dies ist sehr weit entfernt von unseren bei Wellenflügen gewonnenen Erfahrungen, die uns davon ausgehen lassen, dass das ausfliegbare Steiggebiet der Welle luvwärts vor der senkrechten Achse unter dem Wellenberg liegt, wo sich ggfs. Rotorerscheinungen zeigen. Selbst wenn man anstatt der Geraden eine Sinuskurve betrachtet, wird deutlich, dass schon bei geringeren Wellenlängen und Amplituden größere Steigungen der Wellenströmung eintreten werden. Noch deutlicher, wenn das Wellental mehr einer bauchigen U-Form ((Trochoide) nahekommt.
Wenn wir auch davon ausgehen können, dass die angenommenen Wellenlängen plausibel sind, müssen wir nach diesen Gedanken aber feststellen, dass die Amplitudengrößen nachfolgend wahrscheinlich überschätzt werden.
Insofern ergibt sich hier ein weiterer Unsicherheitsfaktor für die nachfolgenden Betrachtungen.

für die Welle am großen Ith-Krücken Steinbruch mit unbekanntem Auslöser:
Phase 1: ca.    1 m/s, sin = 0,066666667, Anstiegswinkel = 3,82°, also ca.  4°
Phase 2: ca. 2,5 m/s, sin = 0,166666667, Anstiegswinkel = 9,55°, also ca. 10°
Phase 3: ca. 1,2 m/s, sin = 0,08,             Anstiegswinkel = 4,58°, also ca.   4,5°
für die Schaumburg-Welle:
Phase 1: ca.    1 m/s, sin = 0,066666667, Anstiegswinkel =  3,82°, also ca.  4°
Phase 2: ca.    3 m/s, sin = 0,2,               Anstiegswinkel = 11,46°, also ca. 11,5°
Phase 3: ca. 1,1 m/s, sin = 0,07333333,   Anstiegswinkel =    4,2°, also ca.  4°

Die Wellenlänge (Scorer Length) oberhalb der Inversion beträgt ca. 6 km. Die Wellenlänge innerhalb der Inversion ist irrelevant, da die Inversion als Ganzes schwingt (Scale des Phänomens!). Unterhalb der Inversion findet sich weitgehend eine neutrale Schichtung, die keine Oszillationen erlaubt.
Bei der Berechnung der Amplituden für die 6 Situationen müssen wir beachten - wie die Prinzipskizze zur Trigonometrie (oben) in ihrem Bezug zur eingezeichneten Welle verdeutlicht - dass die Strecke, über die der Luftmassenaufstieg sich vollzieht (vom Wellental auf den Wellenberg), die halbe Wellenlänge ist (also 3.000 m) ist. Das Ergebnis unserer Berechnung wird der doppelte Wert der Amplitude sein. Sie ist definiert als Strecke zwischen dem Gleichgewichtsniveau und dem Wellenberg, bzw. dem Gleichgewichtsniveau und dem Wellental.

Es errechnen sich folgende Amplitudenwerte:
für die Welle am großen Ith-Krücken Steinbruch mit unbekanntem Auslöser:
Phase 1: ca. 100 m
Phase 2: ca. 250 m
Phase 3: ca. 120 m
für die Schaumburg-Welle:
Phase 1: ca.100 m
Phase 2: ca.300 m
Phase 3: ca.110 m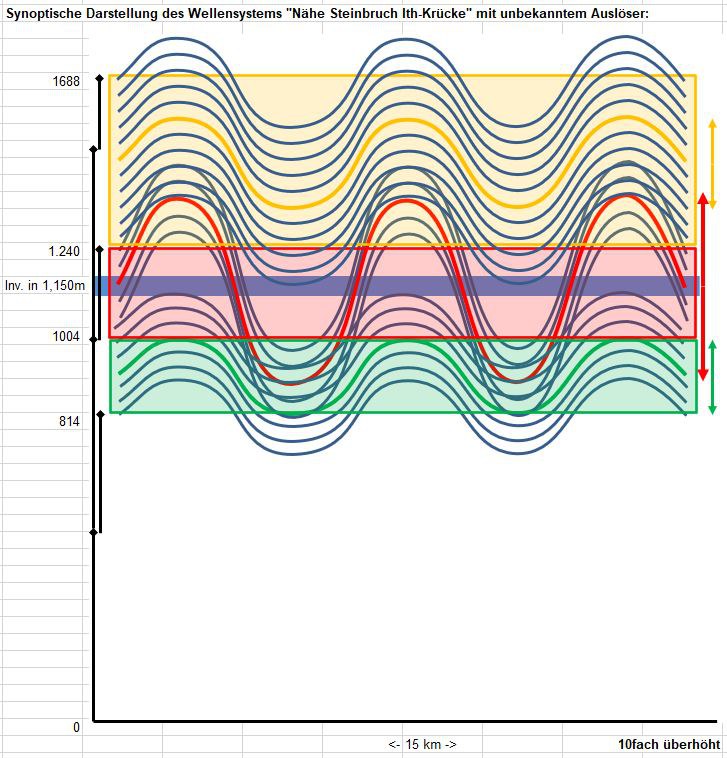

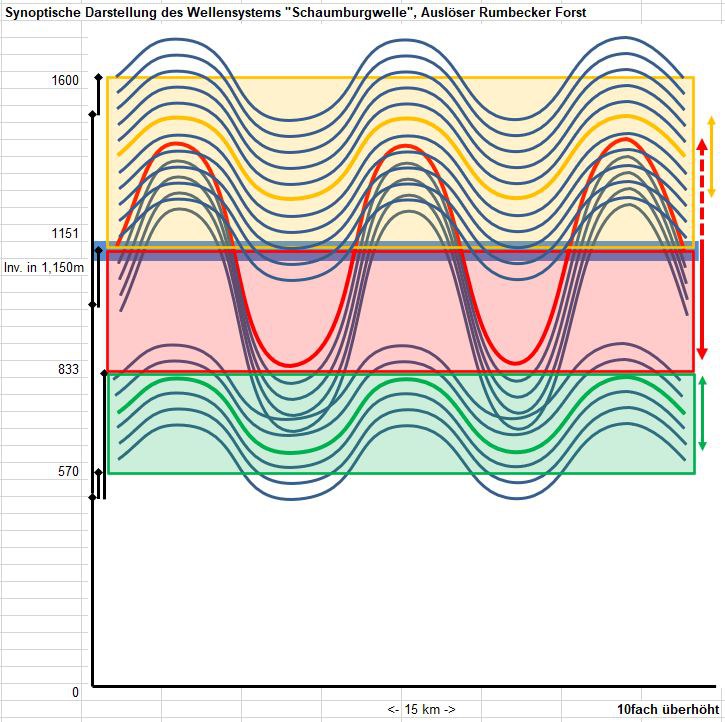
Die Strukur der beiden erflogenen Wellensysteme weist erstaunliche Unterschiede auf:

Die großen Amplituden der Ith-Steinbruch-Welle sind in der Höhe der Inversion und ungefähr symmetrisch zu dieser angeordnet, wobei die Wellental-Amplitude gegenüber der Wellenberg-Amplitude etwas mehr betont ist. Die Amplitudengröße sowie der Bereich in dem das stärkste Luftmassensteigen auftritt, sind kleiner als bei der Schaumburgwelle.
Der untere Bereich mit - zur Schaumburgwelle - vergleichbaren Amplituden ist hier erst ab ca. 800 m erflogen. Es ist nicht bekannt, ob er sich hier auch bis hinab in eine Höhe von ca. 600 m erstreckte.
Die Schicht oberhalb der Inversionsschwingung weist bei beiden beiden Wellensystemen ähnliche Amplitudengrößen in einem Bereich ähnlicher Mächtigkeit auf. Sie wurden in der Ith-Steinbruch-Welle um etwa 100 m höher ausgeflogen, als die der Schaumburgwelle, was keine Aussage darüber trifft, wie hoch die Welle in beiden Fällen tatsächlich reichte. Während der Flugweg in der Schaumburgwelle eher auf einen Abbruch des Steigfluges hindeutet, scheint es bei der Ith-Steinbruch-Welle eher ein "Austoppen" zu sein

Das Frappierende ist aber nun, dass die großen Amplituden der Inversionsschwingung bei der Schaumburgwelle vollständig asymmetrisch ausgebildet zu sein scheinen: direkt oberhalb der Inversion herrschen die kleineren Amplituden des oberen Bereichs vor. Unterhalb aber dominieren - mit größerer Amplitude und sich über einen größeren Höhenbereich erstreckend als bei Ith-Steinbruch-Welle - die großen Wellental-Amplituden des mittleren Bereichs. Die großen Wellenberg-Amplituden des mittleren Bereichs scheinen die Schicht oberhalb der Inversion nicht zu beeinflussen.
Unterhalb der mittleren Schicht finden sich - vergleichbar zur Ith-Steinbruch-Welle - Schwingungen mit kleineren Amplituden, die hier ab 570 m erflogen wurden.

Hier sollte zunächst gut überlegt werden, ob diese Situation nicht einfach ein Artefakt ist, das sich aus den mit der Vorgehensweise bei der Auswertung verbundenen Ungenauigkeiten ergeben haben könnte.
Für die Abgrenzung der unterschiedlichen Steigphasen gegeneinander gilt dies naheliegenderweise. Nach mehrmaliger kritischer Überprüfung der Zuordnung von Loggerpunkten zu den Phasen würde ich dafür aber eine hinlängliche Zuverlässigkeit konstatieren wollen.
Eine Fehleinschätzung der Amplitudengröße scheint mir hier keinen gerichteten Einfluss zu haben, der etwa die Größe der Wellenbergamplitude unterschätzt und die der Wellentalamplitude überschätzt.
Auch erscheint es mir unwahrscheinlich, dass die höheren Steigwerte im mittleren Bereich anders als durch Wellensteigen bedingt worden sind. Die Flugwege scheinen dies zu belegen, wenn auch nicht ausgeschlossen werden kann, dass hier evtl. schubweise "rotoriges" Steigen mitgewirkt haben könnte - wobei Einflüsse thermischer Konvektion wenig bis gar nicht relevant erscheinen. Hier wären natürlich Informationen von den Piloten hilfreich...

M.E. lässt sich diese Situation, wenn man sie wie in den Synopsen dargestellt annimmt, auf zweierlei Weise deuten:
Entweder haben wir es mit Wellen unterschiedlicher Genese zu tun oder wir nehmen im Fall der Schaumburgwelle eine zu große Inversionshöhe an.

Um auch bei der Schaumburgwelle eine symmetrische Anordnung der großen Amplituden der mittleren Schicht - was grundsätzlich, wie am Ith vorgefunden, wohl zunächst die plausiblere Variante ist - annehmen zu können, müsste die Inversion hier flächenhaft um ca. 150 m niedriger liegen als bei der Ith-Steinbruch-Welle. Anders ausgedrückt müsste die Inversion als Bezugsebene für symmetrischen Wellenberg- und Wellentalamplituden hier 150 m niedriger liegen als am Ith. Es geht dabei also nicht um örtliche vertikale Auslenkungen der Inversionsfläche in dieser Größenordnung, sondern um ihre Funktion als Bezugsfläche für eine symmetrische Schwingung.
Das halte ich für weniger wahrscheinlich.

Auch wegen des Fehlens eines probaten Auslösers bei der Ith-Steinbruch-Welle würde ich davon ausgehen, dass es sich hierbei um eine Wellenbewegung handelt, die ihre Quelle in größerer Entfernung luvwärts hat oder/und ein Superpositionsprodukt ist. Auslenkende Kräfte und rückstellende Kräfte mögen sich hier über die längere Lebensdauer der Welle in einem Gleichgewicht eingependelt haben, dass die zugehörigen Amplituden symmetrisch bezogen auf die Inversion angeordnet erscheinen lässt. Eine verbleibende Abweichung davon mag in der ebenfalls asymmetrischen Schichtung - oben stabiler als unten - begründet sein. Welche Größenordnung dieser dadurch bedingte Effekt annehmen kann, entzieht sich meiner Kenntnis.

Bei der Schaumburgwelle hingegen erscheint es (mir) als eher wahrscheinlich, dass sie sich als aktuell im Auslösungsprozess befindlich darstellt - und zwar in einem solchen, der Wellentalamplituden der Inversion zur Folge hat. Dies kann durch Druckfall im Gebiet des Triggers verursacht sein.
Grundsätzlich gestützt wird dieser hypothetische Ansatz dadurch, dass sich die Amplituden im mittleren Bereich als gegenüber denen der Ith-Steinbruch-Welle - durch aktuellen Einfluss des Trigger-Mechanismus - energiereicher zeigen.

Gebirgswellenauslösung

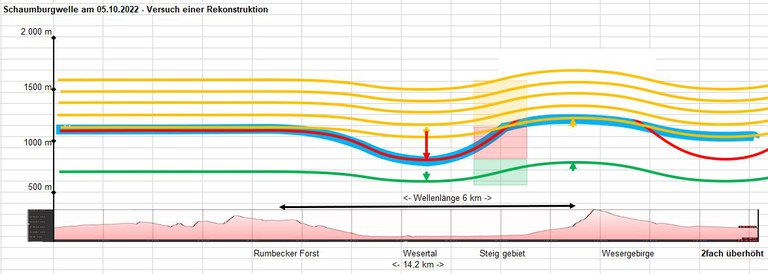
Lage des Geländeschnitts (abweichend von der Höhenwindrichtung 240° hier 225°/045° verlaufend)

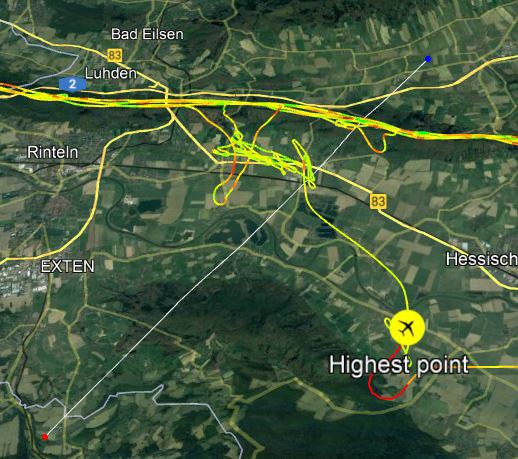
Das verbreitete Denkmodell zur Leewellen-Auslösung stellt sich - nach meinem Verständnis - folgendermaßen dar:

In einer stabil geschichteten Luftmasse, die über ein bewegtes Relief hinweg advehiert wird, stellen sich Geschwindigkeitsunterschiede in der horizontalen Strömung ein. Grundlegend bedingt wird dies dadurch, dass ein Ausweichen der Luftmasse nach oben durch die stabile Schichtung behindert ist. Dies geschieht besonders effektiv, wenn es eine Diskontinuität im Stabilitätsverlauf (Inversion) gibt und diese in nicht allzu großer Höhe über dem dem Relief liegt. Dadurch ergeben sich Verengungen im Strömungsverlauf über Erhebungen (insbesondere wenn sich diese quer zur Windrichtung erstrecken) und Erweiterungen desselben über Tälern.

Die Geschwindigkeitsänderungen können über die im Kontinuitätsgesetz erfassten Zusammenhänge berechnet werden:

Im Bereich der Verengungen im Strömungsverlauf - etwa über Kammlinien, welche sich quer zur Windrichtung erstrecken - kommt es zu einer Beschleunigung der Strömung (vgl. Bild unten), im Bereich von Erweiterungen im Strömungsverlauf - etwa über Talebenen - kommt es zu einer Verlangsamung der Strömung.

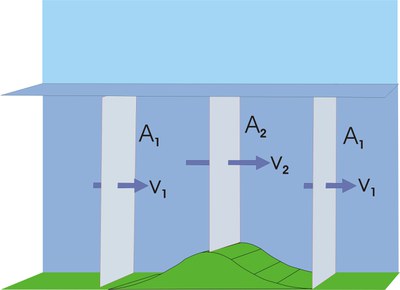
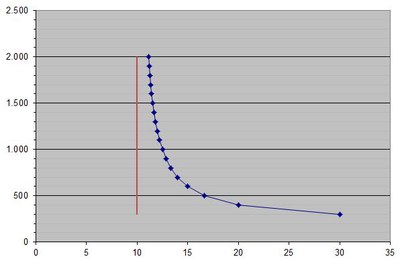
In der folgenden Grafik ist der Versuch dargestellt, diesen Effekt zu quantifizieren. Dabei wird davon ausgegangen, dass Luft in diesem Scale - was die betrachteten Volumina und Geschwindigkeiten angeht - inkompressibel ist.
Die Modellbetrachtung nimmt eine Kammhöhe von 200m über Talniveau an und eine Advektionsgeschwindigkeit von 10 m/s (rote senkrechte Linie). Variiert wird die Inversionshöhe. Ergebnis der Berechnung ist die Strömungsgeschwindigkeit über dem Kamm (blaue Punkte/Linie). Bei einer Inversionshöhe über Tal von 1.000 m ergibt sich z.B. eine Beschleunigung der Strömung auf etwa 12,5 m/s (Diese Modelldimensionen entsprechen ungefähr der Situation vom 05.10.2022).

 Auch an Plateaurändern tritt dieser Effekt entsprechend auf:

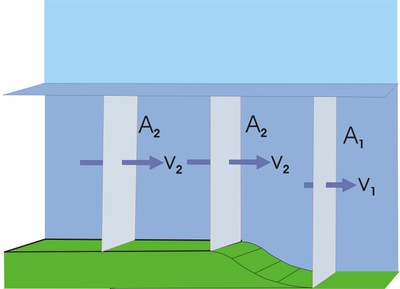
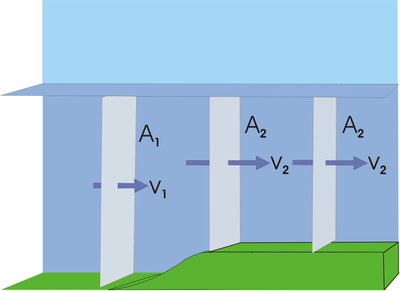
Beschleunigungen und Verlangsamungen der Strömung gehen nach den von Daniel Bernoulli mathematisch formulierten Zusammenhängen mit Druckänderungen einher.
Beschleunigungen führen zu einem Druckfall, Verlangsamungen zu einem Druckanstieg. Insbesondere der Zusammenhang zwischen Beschleunigung einer Strömung und dem einhergehenden Druckfall ist unter der Bezeichnung "hydraulisches Paradoxon" allgemein bekannt. So erklärt sich die Tatsache, dass ein Luftstrom zwischen zwei konvex gewölbt aneingehaltenen Papierblättern diese nicht zum Auseinanderweichen bringt, sondern im Gegenteil diese sich schließlich im Strömungsspalt berühren lässt. Es gibt viele weitere Alltagsbeispiele, bis hin zum Duschvorhang, der ständig nach innen strebt.

Schon das Beispiel von den Papierblättern lässt deutlich hervortreten, dass die geschilderten Abhängigkeiten von Druck und Geschwindigkeit einem positiv selbst verstärkendem Effekt unterliegen. Ein anderes Beispiel verdeutlich dies ebenfalls: Ein Schiff, das in einem Kanal mit "wenig Wasser unter dem Kiel" fährt (und dessen Dimensionen insgesamt groß im Verhältnis zum Kanal sind), läuft Gefahr, ab einer bestimmten Geschwindigkeit auf Grund zu laufen. Die Beschleunigung der Strömung in dem Schlitz zwischen Schiffsrumpf und dem Kanalgrund führt zu einem Druckabfall dort und letztlich zu einem "Festsaugen" des Schiffsrumpfes am Kanalgrund.

Diese Mechanismen lassen sich nun grundsätzlich auf das Verhalten einer Inversion über unebenem Relief übertragen. Die Auslenkung der Inversion nach unten bei Beschleunigung der Strömung und die einhergehenden Selbstverstärkungseffekte scheinen besonders intensiv auftreten zu können, wenn die Stabilität in der Luftmasse unterhalb der Inversion gering ist - wie im betrachteten Fall (05.11.2022).
Dieser Effekt kann aber dennoch die Entstehung von Leewellen nicht abschließend anschaulich erklären, da er sich genau über dem Kamm und nicht etwa am Leehang abspielt. Es wäre interessant, diesen Effekt und sein Selbstverstärkungspotential quanititativ durchzurechnen, ebenso wie die Frage, ob dieser Effekt sich tatsächlich genau über dem Kamm abspielt oder ob es einen leewärtigen Versatz geben kann.

Hinzu kommt ab einem gewissen Grenzwert der Verengung des - hier zweidimensional angenommenen - vertikal begrenzten Strömungskanals zwischen Inversion und Kamm ein weiterer, ebenfalls selbst verstärkender Effekt:
Die Transportkapazität des Schlitzes zwischen beiden reicht irgendwann nicht mehr aus, einer Vergrößerung des Druckunterschieds zwischen Luv- und Leeseite des Höhenzuges entgegenzuwirken. Ab diesem Moment kommen dann sehr große Kräfte ins Spiel. Die Inversion wird weiter herabgesaugt, wobei sich das Zentrum des Unterdrucks an den Leehang verlagert, was wiederum zu einem immer weitergehenden Anschmiegen der Inversion an den Leehang führt. Das wiederum führt zu einer weiteren Beschleunigung der Strömung mit weiterer Verengung es Strömungskanals bei ständiger weiterer Vergrößerung des Druckabfalls im Leebereich des Gebirgszuges. Was wir erleben sind dann Föhnstürme ("Downslope windstorms") von großer Intensität (wie sie auch z.B. vom Ith in Ostwellen-Situationen geschildert wurden). Das sind dann auch die Situationen in denen die Strömung irgendwann in einem hydraulischen Sprung "explodiert".

Bevor dieses Klimax-Stadium des Systems eintritt, also noch in weniger energiereichen Ausprägungen des Systemverhaltens, beobachten wir im Anschluss an die Beschleunigung der Strömung am Leehang durch die nachfolgend (leewärts) auftretende Aufweitung des Strömungskanals eine Abbremsung der Strömung und einen einhergehenden Druckanstieg. Dies ist dann das Gebiet, in dem die kinetische Energie des Leehangströmung in die Form der potentiellen Energie überführt wird und die vertikale Auslenkung der den Leehang herabgesaugten Luftmassen bis in deren Gleichgewichtslage zurück und darüber hinausschießend stattfindet. Wir stellen also fest, dass die Mechanismen der BV-Frequenz nicht nicht nur für "Luftpakete" eingeschlossen in Wetterballons gelten, sondern auch für ganze Wellenberge und -täler. Diese Vorgänge unter dem primären Wellenberg gehen mit dem einher, was wir als "Rotorturbulenz" bezeichnen. Die vertikale Auslenkung von Luftmassen am Leehang nach unten und die einhergehende Beschleunigung dort stellt einen pefekten Auslösemechanismus für Grenzflchen-Wellen dort dar, zeigen doch die Wellen selbst genau dieses Verhalten bei dem Hin- und Herpendeln zwischen den Zuständen von maximierter Potentieller Energie (in den Wellenbergen) und Kinetischer Energie (in den Wellentälern).

Damit haben wir - per Denkmodell - zumindest geklärt, warum es Leewellen geben kann, ohne dass wir eine stabile Schicht in Bodennähe haben. Das Rätsel jener "fernwirkenden" Kraft (vgl.o.) scheint gelöst...

Diese Modellvorstellung auf den hier konkret betrachteten Fall zu beziehen, ist mir allerdings nicht möglich. Dass es bei der gegebenen Schichtung keiner übergroßen Kräfte bedürfen mag, die Inversion in der festgeslellten Form nach unten auszulenken erscheint als plausibel. Damit ist auch die festgestellte Verteilung des Wellensteigens einigermaßen plausibel.
Nicht automatisch organisch zuordenbar scheinen mir aber die beiden oben (hypothetisch!) dargestellten Auslöseprozesse: die größte Auslenkung der Inversion nach unten tritt hier - wie erwartet! - über dem Wesertal auf, was ein direktes Wirken des ja im Kammbereich geschwindigkeitsbedingt auftretenden Bernoulli'schen Druckfalls ausschließt. Andererseits scheint es nicht plausibel zu sein, annehmen zu können, dass die Transportkapazität der zwischen Kamm des Gebiets "Rumbecker Forst" und der Inversion resultierenden Verengung tatsächlich eine so weit gehende Einschränkung erfahren haben sollte, dass es dadurch zur Ausbildung einer Druckdepression im Bereich des Leehangs gekommen sein könnte.
Im Konzert der Kräfte spielen allerdings die ohnehin im Lee erniedrigten lokalen Drücke auch ihre Rolle. Sie zeigen sich augenfällig in vergleichsweise abgemilderter Form, sogar auch bei labilen zyklonalen Lagen, z.B. in den sich häufig auf halber Lee-Hanghöhe bildenden Wolkennebeln, die sich nicht selten in durch eben solche Druckunterschiede erzeugten Leewirbeln drehen.

Ganz sicher spielt an diesem Tag eine Rolle, dass in der herangeführten Luftmasse bereits Wellenbewegungen stattfanden, die In Phase mit dem Relief des Gebiets Rumbecker Forst gestanden haben mögen. Diese wurden  außer Acht gelassen. Stellen sie hier doch eher einen "Black Box"-Ansatz dar, der die detailliertere Problemlösung nur verlagert.

Doch gerade diese offenen Fragen sind ja das Faszinierende... und so gibt es neben dem des Segelflugs auch das Abenteuer "Wissenschaft".
Und ich bin gespannt, welche Bilder sich in diesem Auswertungsraster an anderen Wellenflugtagen zeigen werden...